Astronomers at the University of Texas-Austin are using the ideas of Charles Darwin to learn about the interior of white dwarf stars—using a minimal parallel Linux cluster tailored specifically to their application.
Astronomers worry about how stars work. Our current models describe stars as huge, hot gasballs, bloated and made luminous by a fusion furnace deep inside that burns hydrogen into helium and releases energy in the process. A kind of internal thermostat keeps them stable, so our planet enjoys a comfortable environment in its orbit around our star, the sun. In about 6,000 million years or so, all available fuel will be burned up, and as the fuel gets low, the sun will bloat, then shrink until it is 100 times smaller than it is now, becoming a white dwarf star. Written inside, in the ashes of the furnace, will be its nuclear history.
We have pieced together this story by looking at many different stars, which last much longer than we do, but we cannot see inside any of them. Stars are very luminous yet thoroughly opaque. Geologists have built up a detailed picture of the earth’s interior, even though it is opaque too; they do this by watching as compression waves from earthquakes rattle around inside and make their way back to the surface: seismology. By a very fortunate circumstance, we have found that some white dwarf stars vibrate internally with something akin to earthquakes, all the time. Their rapid changes in brightness tell us what is going on inside: asteroseismology.
To take advantage of this cosmic bonanza, we build computer models of the stars, with adjustable parameters that reflect, one-to-one, the physics going on inside. We must “vibrate” our model and tweak its parameters until the model behaves like a real star. We then believe that the parameters in our model tell us about the physics inside the white dwarf star. We can then start to read the history written there.

Figure 1. Evolving Penguin
Evolving Darwin
The basic idea is nifty, but the practice is a bit complicated. The models have many parameters, not all independent of one another, and we are not completely sure we have all the physics right. To make sure the set of model parameters we use is the best fit to the observed behavior and the only reasonable one, we have to explore a very large, multi-dimensional parameter space—far too large and complex to examine in exhaustive detail. No existing computer could handle it. There is a way though: we populate our huge parameter space at random with models whose parameters cover the whole shebang. Then we breed them together, preferentially allowing those which fit the observations fairly well to survive into later generations. This survival of the fittest is done with a “genetic algorithm” that mimics, in a crude but effective way, the process of natural selection proposed by Charles Darwin.
Genetic Algorithms
The underlying ideas for genetic algorithms were inspired by Charles Darwin’s notion of biological evolution through natural selection. The basic idea is to solve an optimization problem by evolving the best solution from an initial set of completely random guesses. The theoretical model provides the framework within which evolution takes place, and the individual parameters controlling it serve as the genetic building blocks. Observations provide the selection pressure.
Parallel Genetic Algorithm Chart
Initially, the parameter space is filled uniformly with trials consisting of randomly chosen values for each parameter, within a range based on the physics the parameter is supposed to describe. The model is evaluated for each trial, and the result is compared to the observed data and assigned a fitness inversely proportional to the variance. A new generation of trials is created by selecting from this population at random, weighted by fitness.
In order to apply genetic operations to the new generation of trials, their characteristics must be encoded in some manner. The most straightforward way of encoding is to convert the numerical values of the parameters into a long string of numbers. This string is analogous to a chromosome, and each number represents a gene. For example, a two-parameter trial with numerical values x1=1.234 and y1=5.678 would be encoded into the single string of numbers 12345678.
Next, the encoded trials are paired up and modified in order to explore new regions of parameter space. Without this step, the final solution could ultimately be no better than the single best trial contained in the initial population. The two basic operations are crossover which emulates sexual reproduction and mutation which emulates happenstance and cosmic rays.
As an example, suppose the encoded trial above is paired up with another trial having x2=2.468 and y2=3.579, which encodes to the string 24683579. The crossover procedure chooses a random position between two numbers along the string and swaps the two strings from that position to the end. So, if the third position is chosen, the strings become
123|45678 -> 123|83579 246|83579 -> 246|45678
Although a high probability of crossover exists, this operation is not applied to all of the pairs; this helps keep favorable characteristics from being eliminated or corrupted too hastily. To this same end, the rate of mutation is assigned a relatively low probability. This operation allows for spontaneous transformation of any particular position on the string into a new randomly chosen value. So if the mutation operation were applied to the sixth position of the second trial, the result might be:
24645|6|78 -> 24645|0|78
After these operations have been applied, the strings are decoded back into sets of numerical values for the parameters. In this example, the new first string 12383579 becomes x1=1.238 and y1=3.579 and the new second string 24645078 becomes x2=2.464 and y2=5.078. This new generation replaces the old one, and the process begins again. The evolution continues until one region of parameter space remains populated while other regions become essentially empty.
It works far better than we had expected before trying it.
Even using this trickery, a lot of computing is required, so we built a massive parallel system to cut the runtime to hours instead of weeks. Most of the model calculations are done in floating-point arithmetic, so we measure performance in flops, the number of floating-point operations per second. Our assembled system, called a metacomputer, is capable of more than two gigaflops—2,000 million floating-point operations per second—not bad for an assembly of Linux boxes.
Our strategy in designing this system was minimalist; keep each computer node as cheap and simple as possible, consistent with doing our job and getting the maximum amount of computing for the buck. Our budget is fairly limited. CPU cost is not a linear function of speed, so you pay a great deal more per megaflop for the fastest CPU on the market. Older CPUs are cheaper, but require more boxes and supporting electronics to house them for the same final performance. We watched the price drops with avid interest and jumped just after the 300MHz Intel P-II dropped below $300. We could afford a good master control computer and 32 computing nodes with our $22,000 budget.

Figure 2. Computer Lab
Some time after we settled on the design, we became aware of the existence of Beowulf machines through an article in Linux Journal (see Resources)—also parallel systems running Linux, but with faster Ethernet connections and more storage than our problem requires. They are much more general purpose than the system we built, so they can handle many problems ours cannot. They cost more too.
Cheap Hardware, Free Software
Our master computer is a Pentium-II 333 MHz system with 128MB SDRAM and two 8.4GB hard disks. It has two NE-2000 compatible network cards, each connected to 16 nodes using a simple 10base-2 coaxial network. We assembled the nodes from components obtained at a local discount computer outlet. Each has a Pentium-II 300 MHz processor housed in an ATX tower case with 32MB SDRAM and an NE-2000-compatible network card. We used inexpensive 32KB EPROMs, programmed with a BP Microsystems EP-1 using a ROM image from Gero Kuhlmann’s Netboot package, allowing each node to boot from the network.
Table 1. Hardware components for minimal nodes
| Component | Justification |
| Pentium-II 300MHz processor | Peak performance/cost for this configuration |
| CPU fan | Required for Pentium-II |
| LX motherboard | Least expensive chipset supporting 300MHz |
| ATX tower case | Includes power supply for Pentium-II, etc. |
| 32MB SDRAM | 8MB RAM disk plus sufficient memory for our code |
| PCI 10MB Ethernet card | Low bandwidth Master-Node communication only |
| 32KB EPROM | Least expensive boot option |
| 3-ft Coaxial cable | Simple network without repeaters or hubs |
Configuring the software was not much more complicated than setting up a diskless Linux box (see Robert Nemkin’s Diskless Linux Mini-HOWTO). The main difference was that we minimized network traffic by giving each node an identical, independent file system rather than mounting a shared network file system. Since the nodes had no hard disks, we needed to create a self-contained file system that could be mounted in a modest fraction of the 32MB RAM.
To create this root file system, we used Tom Fawcett’s YARD package (http://www.croftj.net/~fawcett/yard/). Although Yard was designed to make rescue disks, it was also well-suited for our needs. We included in the file system a trimmed-down, execute-only distribution of the PVM (parallel virtual machine) software developed at Oak Ridge National Laboratory (http://www.epm.ornl.gov/pvm/). PVM allows code to be run on the system in parallel by starting a daemon on each node and using a library of message-passing routines to coordinate the tasks from the master computer.
We configured the master computer to be a BOOTP/TFTP server, allowing each node to download the boot image—essentially a concatenation of a kernel image and a compressed root file system. We used the Netboot package (http://www.han.de/~gero/netboot/) to create this boot image using the root file system created by YARD and a small kernel image custom-compiled for the nodes.
How It Works
With the master computer up and running, we turned on each node one at a time. By default, the BIOS in each node tries to boot from the network first. It finds the boot ROM on the Ethernet card, and the ROM image broadcasts a BOOTP request over the network. When the server receives the request, it identifies the associated hardware address, assigns a corresponding IP address, and allows the requesting node to download the boot image. The node loads the kernel image into memory, creates an 8MB initial RAM disk, mounts the root file system, and executes an rc script which starts essential services and daemons.
Once all nodes are up, we log in to the server and start the PVM daemon. An rhosts file in the home directory on each of the nodes allows the server to start up the daemons. We can then run in parallel any executable file that uses the PVM library routines and is included in the root file system.
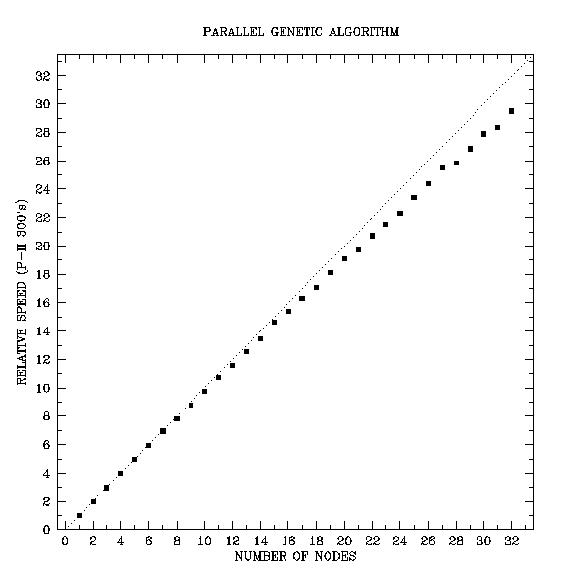
For our problem, the executable residing on the nodes involves building and vibrating a white dwarf model and comparing the resulting theoretical frequencies to those observed in a real white dwarf. A genetic algorithm running on the master computer is concerned with sending sets of model parameters to each node and modifying the parameter sets based on the results. We tested the performance of the finished metacomputer with the same genetic algorithm master program as our white dwarf project, but with a less computationally intensive node program. The code ran 29.5 times faster using all 32 nodes than it did using a single node. Our tests also indicate that node programs with a higher computation to communication ratio yield an even better efficiency. We expect the white dwarf code to be approximately ten times more computationally intensive than our test problem.
Stumbling Blocks
After more than three months without incident, one of the nodes abruptly died. As it turned out, the power supply had gone bad, frying the motherboard and the CPU fan in the process. The processor overheated, shut itself off, and triggered an alarm. We now keep a few spare CPU fans and power supplies on hand. This is the only real problem we have had with the system, and it was easily diagnosed and fixed.
Conclusions
The availability of open-source software like Linux, PVM, Netboot and YARD made this project possible. We would never have considered doing it this way if we’d had to use a substantial fraction of our limited budget to buy software as well as hardware and if we’d been unable to modify it to suit our needs once we had it. This is an aspect of the Open Source movement we have not seen discussed before—the ability to try something new and show it can work, before investing a lot of money in the fond hope that everything will turn out fine.
 Linux, Linux OS, Free Linux Operating System, Linux India Linux, Linux OS,Free Linux Operating System,Linux India supports Linux users in India, Free Software on Linux OS, Linux India helps to growth Linux OS in India
Linux, Linux OS, Free Linux Operating System, Linux India Linux, Linux OS,Free Linux Operating System,Linux India supports Linux users in India, Free Software on Linux OS, Linux India helps to growth Linux OS in India